いつかは自然災害の予測も。身の回りに潜む“災い”を数理モデルで予測・制御する「防災数学」への期待

事故、災害、病気、けが……。ある日突然訪れる、さまざまな「災い」。それらを完全に避けることは不可能ですが、それでもできる限り予測を立て、リスクを最小限に抑えられるに越したことはありません。そこで、市田優先生が取り組んでいるのが「防災数学」という新しい研究領域。「広い意味での災い」に備えるための数理的アプローチについてお話を伺いました。

数学と「防災」がつながったコロナ禍の体験

「防災数学」という耳慣れない言葉。市田先生が、博士後期課程の指導教員だった矢崎成俊先生（明治大学）とともに提唱してきた新しい学際研究領域です。

「防災というと、地震や台風への備えがまず想像されるでしょう。もちろんそうしたスケールの大きな災害も扱っていきたいですが、それだけに限らず、病気や事故、大小さまざまな『災い』を防ぐことを目的としてその背景にある各分野の専門家と共同研究を行っています。誤解を招かないように、そしてより身近に捉えていただけるように、『広い意味での災い』と紹介することもあります」

そもそも、数理モデルと現象の数理解析を研究する市田先生が、防災を意識するようになったきっかけは、なんだったのでしょう。そうたずねると、コロナ禍に目の当たりにした研究者たちの奮闘だったと市田先生は答えます。

「新型コロナウイルスの感染拡大で世の中が混乱していた当時、私は博士前期課程の学生で、大学に行くこともできず家に引きこもっていました。そんなときに、コロナの流行を収めるために人との接触を8割減らすことが必要と示し『8割おじさん』と呼ばれた京都大学の西浦博先生をはじめ、積極的に発信をされている専門家の方々を見て、自分も数理モデルを使って世の中のためにできることはないかと考えたんです」

数理モデルとは複雑な要因が絡み合う自然や社会の現象を、数学の式で表そうとするもの。そして市田先生が取り組んだのが、感染者数がどう推移するかという未来予測の数理モデルでした。

「コロナウイルスを一人の感染者が何人に感染させるかという値を基本再生産数といいます。この値を用いて未来予測の数理モデルが多く提案されています。私はある典型的なモデルが持つより豊かな構造を引き出す数学解析を行いました。この研究を通して、社会に対する強いメッセージを打ち出す結果までは得ることはできませんでしたが、数理のアプローチから人の役に立つ研究をしたい、そのためには広く実験と数理が織りなす分野横断的なアプローチの推進が必要だという思いが生まれました。今振り返ると、現在取り組んでいる『防災数学』につながっている気がします」

本質を捉えた数理的アプローチで、ペースト状人工骨の開発に貢献

さまざまな分野の専門家と、さまざまな「災い」を防いだり、取り除いたりする研究に取り組んでいる市田先生。現在力を入れているのは、意外なことに人工骨の研究だそうです。骨に生じる災いとはいったい、どういうものでしょう。

「骨粗鬆症などが原因で欠損した骨を補う人工骨というものがあります。現在、整形外科では自家骨移植、すなわち患者自身の健康な骨の一部を採取して欠損部を補う方法がなされていますが、この方法はとくに高齢者にとっては負担が大きく、再骨折のリスクもあります。そこで注目されているのが、欠損部に歯磨き粉のようなペースト状の素材を注入し、その素材が次第に患者さん自身の骨に置き換わるように促すという治療法です。ペースト状人工骨では、骨への置き換わりやすさ、抗菌性などさまざまな基準を考慮した物質の配合が肝になりますが、その基準の一つに『亀裂や空隙が発生しない』という条件があります。注入したペーストは体内で膨らんで欠損部を埋めるように設計されているのですが、その際に亀裂や空隙が生じると、再骨折の原因になってしまうのです。

亀裂や空隙が発生しづらい配合についてはすでに研究が進んできてはいるのですが、その根底となる『なぜ亀裂や空隙が発生するのか/しないのか』という仕組みまでは明らかになっていませんでした。実際に治療に使用するための安全性を確認し、さらに強靭な人工骨を開発するためにも、そのメカニズムの解明が課題となっているそうです。このメカニズムはペースト状人工骨の実験の世界では推測の域では考察が与えられているそうなのですが、数式でバチっと言えたらかっこいいと思い、実験と数学チームがコラボして議論を進めています」

この場合、ペースト状人口骨の亀裂や空隙の発生が、「災い」ということですね。では、その「災い」の発生率を減らすために、どのように数学を使ってアプローチをするのでしょうか？

「このペースト状人工骨の開発を行う研究者とタッグを組んで共同研究に取り組んでいます。まずは実験見学させていただきました。実際にこの手でペーストをこねてから、注射器に詰めて模型に注入する体験もしました。それからペースト状人工骨の最新の研究をレクチャーしてもらい、関連する論文も読み込みました。言葉を知るところからのスタートでした。数理モデルの作り方の王道としては素材となる物質の化学反応式や物理的な性質から数理モデルを作っていくことが一般的ですが、そのように扱える化学式がそもそも存在しないということがわかったので、われわれは少し変わった方法で数理モデルを作っていきました。その結果、人工骨の成分の配合と亀裂や空隙の発生しづらさに関して説得力のあるメカニズムを説明できるようになりつつあります」

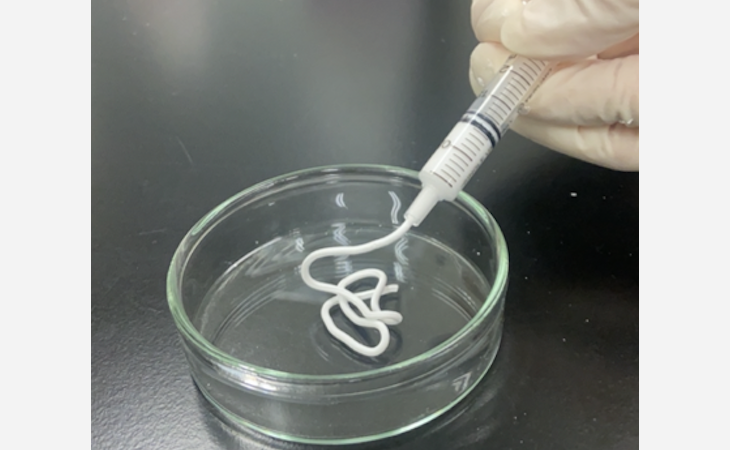
実験で明らかになったことを理論的に裏付けて、臨床現場に応用したり、研究をさらに発展させたりするために数理モデルが有用なのだそう。気になるのは、数理モデルを作るために市田先生が用いた「少し変わった方法」です。

「化学反応など現象の成り立ちから数式を組み立てるのではなく、現象そのものの実験データをよく観察し、すでに知られている方程式のうちこれに当てはめることができるのではないかと予測を立てて、数理モデルに落とし込んでゆくというものです。これをわれわれは現象論的アプローチと呼んでいます。この方法の長所は、現象を成り立たせる詳細な要素がわかっていなくても、現象全体を大きく捉えて妥当なモデルを構築することができる点です。もちろん、ある方程式が偶然当てはまったからといって、それが絶対に正解だとは言いきれません。検証を繰り返し、その精度を上げていくことでモデルの市民権を得ていく過程が重要になります」

市田先生は数理モデルについて、「現象の本質をいかにシンプルに捉えて、そこから複雑な現象の要因を説明できるか」を大切にしていると言います。それは言い換えると、多くの人にとってわかりやすく、本質を突いたメッセージを訴えられるかということ。先生が「少し変わった方法」という現象論的アプローチは、まさにその考え方に通じます。ついついものごとの細部にこだわってしまいがちな私たちにとっても、大いに参考になる視点です。

そしておもしろいことに、一見関係のなさそうに見える現象同士が実は同じ方程式で表すことができてしまう、ということも起こるのだとか。さまざまな現象の背後に、実は宇宙の法則とでも言いたくなるようなルールがあると考えると、なんともロマンを感じてしまいます。

「もちろん、一つの数式ですべてが語れるわけではありませんが……。既知の方程式は解析の結果もおおよそ知られているので、ある意味ではリーズナブル、かつ数学の研究成果としてインパクトも与えられるという実利的な側面もあります」

電子部品、害虫対策、医療。分野融合によって広がる可能性

興味を持ったテーマを自身で調べることもあれば、他分野の専門家から相談を受けて共同研究に発展することもあるという市田先生。他にもさまざまな「防災」について研究を進めています。

「最近私の中で盛り上がっている研究は、スマートフォンやパソコンなどの身の回りの機械に内蔵されているMEMS（メムス、微小電気機械システム）に関する研究です。ものすごく小さな部品ですが、機械のパフォーマンスに大きく関わっているそうです。先日、MEMSに関する実験を行っている先生の研究室を訪問し、MEMSを実際に見せていただきました。MEMSの性能をアップさせるために数理モデルを構築して、理論的に性能アップへのMEMSの実装方法を提案する研究に最近取り掛かりました。これは未来志向の防災数学といったところでしょうか。性能をあげることで起こるかもしれない災いを防ぐ。うまくいけば、将来自分の数学が設計したものが内蔵された電子機器を使って高いパフォーマンスができるのが楽しみです」

害虫駆除に関する研究も行っていると、話を続ける市田先生。数理モデルを害虫駆除に役立てるとは、想像がつかないのですが……。

「伝染病を媒介する蚊は、地域によっては非常に危険な生き物です。ある一帯で大規模に蚊を駆除しようとした場合に、遺伝子操作で不妊にした蚊を放って繁殖を抑制することで個体数を減らすという方法が知られており、実際に成功例も知られています。しかし放出すれば必ず個体群抑制に成功する保証はないので、実施する場合、どれくらいの量の蚊をどんな条件で放ったら効果があるのかという予測が不可欠です。そうした政策提言のための研究を数学者同士で進めていて、こちらもゆくゆくは蚊の専門家を交えて実用的なものにしていきたいと考えています」

お話を聞くと感染症も電子部品も害虫も、どれも分野は異なるものの、たしかに「広い意味での災い」。最後に、今気になっているテーマをお聞きしたところ、「血管新生の数理モデル」について説明してくれました。

「血管新生とは、既に存在する血管のネットワークから出現する新しい血管とその血管を構成する形態形成現象。けがをしたときに起こり、これにより傷口は回復に向かいます。がんの転移にも血管新生が関わっているとされているのですが、メカニズムの完全な理解は医学的にもまだなされていないとか。血管が新しくできるメカニズムを解明することで、数学からの医学への貢献ができるのではないかと考えています。生命現象は非常に複雑なので、数理モデルで表すのも簡単ではありませんが、いつか共同研究者を見つけて挑戦したいと考えています」

多岐にわたる分野で活躍が期待され、多くの分野と数学をつなげる架け橋となることが期待される防災数学ですが、数理モデルで示すことができる範囲には限界もあると市田先生は言います。

「数理モデルでできるのは、『こうすればうまくいくのではないか』といった定性的な方針を示すことまでで、たとえばある材料を何グラム添加すればうまくいく、といったような定量的な提言は得意ではないんです。定量的にデータを扱うことに関しては、データサイエンスのほうが適しています。

『防災』を謳っている以上、いつかは台風や津波といった災害を高精度で予測できる数理モデルを作ることは大きな目標ですが、そこでもやはり、鍵になるのはデータサイエンスとの融合だと思います。各分野の専門家による実験と数理モデル、それにデータサイエンスが組み合わさることで、かなりの精度での『防災』が可能になるでしょう」

「防災」という視点を通して、数学を身近に感じてほしい

他分野との融合によって真価を発揮する防災数学。昨年からは定期的に研究集会を主催するなど、その裾野を広げる活動にも積極的に取り組んでいるそうです。なぜ市田先生は防災数学という新しい言葉、研究分野にこだわるのか、その理由をお聞きしました。

「今、学部１回生の数学の授業を担当していまして、いろいろな学部の学生がいる中で『数学を嫌いにならないでほしい』という一心で教えています。学生たちにとっては私の講義が人生で最後の数学の授業になるかもしれないので、せめて少しでもハッピーな印象を持ってもらいたいんです。そうしたときに、たとえばハイパボリックコサインという耳慣れない関数が、吊り橋を支えるケーブルのたわみや飲食店のロゴ、Tシャツの襟首まであらゆるところに現れているという話をすると、すごく親近感をもってもらえるんです。」

防災数学に関しても、難解に思われがちな数学が実は身近なものであり、日常を少しでもハッピーにできる素養を持っていると知ってもらうことで、なるべく分野間の壁を小さくしたいという思いがあります。すでに『現象数理学』という分野があるのですが、そこに『災いを防ぐ』という具体的な目標がある防災数学はさまざまな分野と協業しやすくなるのではないかという個人的な期待があります。多くの人に、自分と関係があることだと思ってもらえる入り口が、『防災』という言葉なのかなと思います」

取材対象：市田 優（関西学院大学理学部 助教）
ライター：谷脇 栗太
運営元：関西学院 広報部
※掲載内容は取材当時のものとなります